Controlar el consumo residual de alimentos es mantener el equilibrio (Parte II)

Definición

Aunque existen diferentes formas matemáticas de estimar la eficiencia alimenticia, la ingesta de alimento residual (RFI) es hoy en día la más utilizada. 

Ventajas e inconvenientes del método

Una de las principales ventajas es, en contraste con rasgos de proporción como la tasa de conversión alimenticia, es la ausencia de correlación entre el rasgo de eficiencia y sus predictores como la producción de leche o el peso corporal (clásicamente a nivel fenotípico, pero también propuesta a nivel genético por Kennedy et al., 1993). 

Esto es particularmente interesante para fines de selección genética (Berry y Crowley, 2013). Sin embargo, persisten algunos problemas con este enfoque. 

El primer problema está relacionado con el uso de coeficientes lineales estáticos en la ecuación de regresión.

Cuando se aplica a animales lactantes, esto no refleja la realidad biológica de los diferentes procesos que ocurren en diferentes etapas de la lactancia, como la movilización de la reserva corporal en la lactancia temprana o la acumulación de reservas asociada con la preñez en la lactancia tardía. 

Por lo tanto, la estimación de RFI durante toda la lactancia con una regresión lineal conduce a evaluaciones sesgadas (Li et al., 2017). 

Varios estudios han explorado más a fondo la metodología de RFI o las relaciones entre sus componentes (por ejemplo, Manzanilla Pech et al., 2014; Strathe et al., 2014; Lu et al., 2015) que condujeron recientemente al desarrollo de nuevos métodos basados en modelos de regresión aleatoria multi rasgo que incorporan la dimensión dinámica de los datos y proponen una solución a este primer problema (Islam et al., 2020; Martin et al., 2021b).

Sin embargo, como el número de parámetros a estimar en el modelo es considerablemente mayor que para una regresión lineal clásica, el número de registros requeridos para su estimación es mayor, lo que lleva a un segundo problema.

Los conjuntos de datos de consumo de alimento residual tienden a ser relativamente pequeños debido a la dificultad y el costo de medir la ingesta. 

Además, si se utiliza la ingesta de MS como medida, la estimación de la eficiencia se contamina por las diferentes densidades de energía de alimentación. El uso de una conversión a la ingesta de energía basada en los valores contables también podría introducir sesgos y potencialmente reducir cualquier variación en la eficiencia digestiva (Martin et al., 2021a). 

En el Cuadro 1 se pueden ver vías metabólicas que subyacen al consumo de alimento residual en terneros Charoláis de engorde.

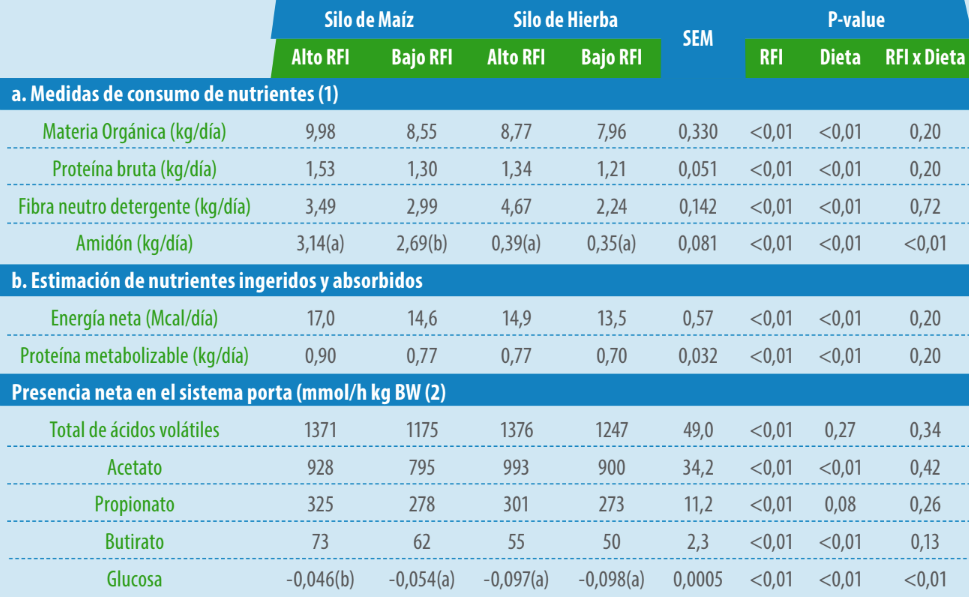a, b: Medidas comparadas sólo con la misma dieta. Diferentes letras significan diferencia significativa de acuerdo a Tukey test (p,05).
1: Medidas basadas en ingestión de materia seca.
2: Estimado de acuerdo con Loncke et al.

Cuadro 1. Vías metabólicas comunes y específicas de la dieta que subyacen al consumo de alimento residual en toros Charolais de un año de engorde

La literatura nos ofrece ideas sobre cómo intentar solucionar este problema. Por ejemplo, Tempelman et al. (2015) y Lu et al. (2017) utilizaron regresiones aleatorias específicas de la ración, de la ingesta de materia seca basados en la energía de la leche y el peso corporal.

Sin embargo, toda la información necesaria sobre la dieta de las vacas no siempre está disponible. Por lo tanto, es útil buscar métodos más simples que puedan usarse al menos dentro de tipos amplios de alimentación en granjas, especialmente cuando se usan metodologías como Martin et al. (2021b) que también aborda el primer problema.

Dejar que el comedero se vacíe no es la solución para reducir los costos de alimentación. Cuando la alimentación está restringida, el pH ruminal puede llegar a ser muy alto (alcalino). Un pH alto inhibe las bacterias que usan el lactato, dejando un ecosistema ruminal susceptible a la acidosis.

En esos momentos, el equilibrio microbiano se rompe y el ganado tiende a comer en exceso cuando se vuelve a ofrecer alimento, lo que aumenta su riesgo de acidosis al comer la siguiente comida abundante. 

Es normal recomendar que los rechazos para el grupo de recién paridas sean de alrededor del 2 al 4%, del 1 al 3% para los grupos de alta producción y del 0,5 al 3% para los grupos de lactancia tardía. 

En general o si se maneja la explotación con lote único de producción, el rechazo de la alimentación no debe exceder del 3 al 4%.

Hay que tener en cuenta que, si los rechazos de alimento son similares en composición al alimento ofrecido, la opción deberán ser porcentajes bajos y si los rechazos son diferentes a lo que se ofrece, se debe optar por los altos. 

Cuanto más diferentes en apariencia y tamaño de partícula son los rechazos del alimento ofrecido, más rechazos deben dejarse para estar seguros, que había alimento de “calidad” disponible si las vacas querían más.

De este tema hay pocas publicaciones científicas concluyentes y muchas recomendaciones sobre las tasas de rechazo de alimento y sus efectos sobre la lactancia. 

Arrimar el alimento varias veces durante al día garantiza que las vacas puedan alcanzarlo fácilmente, lo que puede fomentar la ingesta de alimento y reducir los rechazos.

El modelo se aplicó a los tres conjuntos de datos para estimar la RFI individual, así como los componentes de varianza y las correlaciones entre los cuatro rasgos incluidos en el modelo (producción de leche corregida por grasa y proteína, peso corporal, ingesta de alimento y puntuación de condición corporal), y se utilizó un efecto fijo mes-año-granja para definir el grupo contemporáneo. 

Por lo tanto, el modelo dinámico se puede utilizar para producir estimaciones de RFI a partir de conjuntos de datos combinados, al menos cuando los animales se crían en sistemas similares. Además, las 205 lactancias de la segunda granja también se utilizaron para estimar la RFI con un enfoque lineal. 

La RFI estimada por los dos enfoques fue similar cuando el período considerado fue bastante corto (r = 0,85 para RFI durante los primeros 84 días de lactancia), pero esta correlación se debilitó a medida que crecía la duración del período (r = 0,77 para RFI para los primeros 168 días de lactancia). 

Este debilitamiento en las correlaciones entre los dos enfoques al aumentar el período de tiempo utilizado, refleja que solo el modelo dinámico permite que los coeficientes de regresión evolucionen en línea con los cambios fisiológicos a través de la lactancia. 

Los resultados de este estudio amplían las posibilidades de uso para el modelo dinámico de consumo residual de alimentos. En general, poco a poco los modelos dinámicos se irán usando cada vez más, a pesar de su aparente complejidad.

Te puede interesar Controlar el consumo residual de alimentos es mantener el equilibrio (Parte I)